Count-Min Sketch
This article deep dives into what is count-min sketch as a data structure and how is it helpful in the real world systems
Problem Statement
“How do we count the frequency of any key in a streaming dataset“?
Let's imagine that we have an incoming stream of data and we have to support the following operations:
Insert(key): should increase the key count by value 1.
Query(key): should return the frequency of the key accumulated so far
This problem looks very trivial to solve using the HashMap data structure. We can define a Java HashMap (or similar data structure) to increment the count of every key during the Insert(key) operation and then return the corresponding count for the Query(key) operation.
The main problem here is that as the number of unique keys increases, the HashMap would require too much memory, probably in Megabytes, and would grow linearly with the number of keys.
So, the real question is there a better way to solve this problem that doesn’t use too much memory as the dataset increases? Is there a tradeoff to the proposed solution?
Enters the solution: “Count-Min Sketch”
What is Count-Min Sketch?
Count–Min Sketch (CM sketch) is a probabilistic data structure that serves as a frequency table of events in a stream of data. It helps you to answer a simple query “What is the frequency of a key in the incoming dataset?” with almost constant space storage.
Imagine a grid (referred to as sketch in the algorithm) of w width and d depth. The rows(d) represent the number of hashing functions used and the columns(w) represent the counter array for each of the hashing functions (denoting how many times a key is inserted).
Tradeoff(Space vs Accuracy)
The advantage of using count-min sketch is that it’s a probabilistic data structure. Although it consumes way less memory but it comes at a tradeoff that there is an error rate associated with every output from the count-min sketch. Refer to the the internals to understand it better.
Internals of Count-Min Sketch
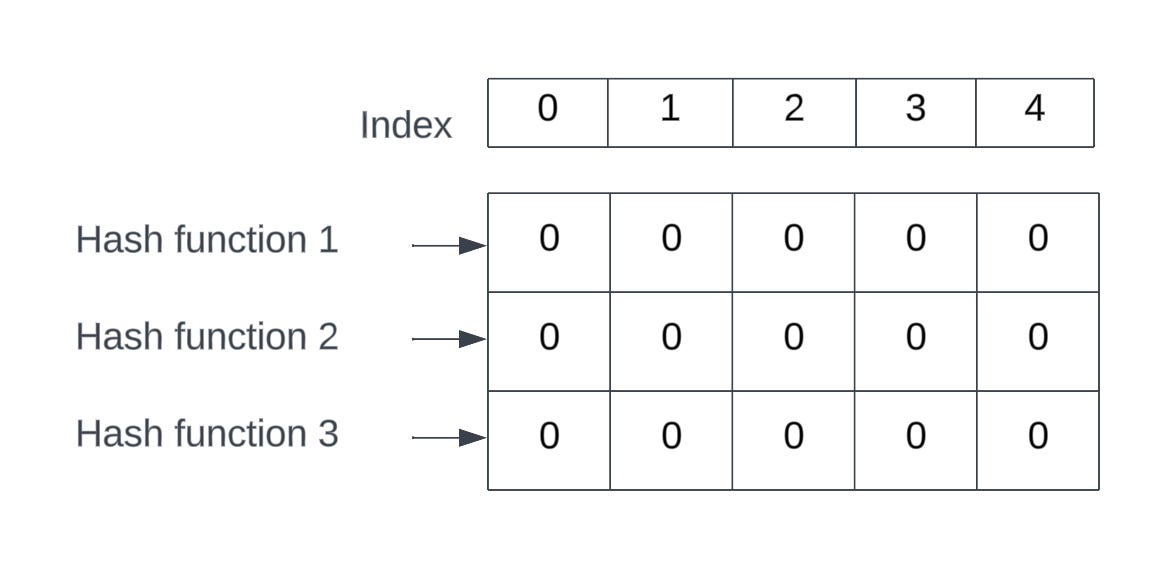
Let’s take an example and break down the steps for each operation. Imagine that we have a sketch(basically a grid) of 3 rows and 5 columns. In this sketch, the rows represent the number of hashing functions and the columns represent the counter array.
Here is the sequence of steps performed for Insert and Query operations.
For Insert(key):
Calculate the Hash(key) of the input key for the number of hashing functions. If we have 3 Hash functions, then compute Hash1(key), Hash2(key), Hash3(key)
Increase the counter by 1 placed on the 0th row and Hash1(key) % 5 column index. Similarly, increase the counter by 1 on the 1st row and Hash2(key)%Y column index and so on for the 2nd row and Hash3(key)%Y column index as well.
Thus, for every incoming Insert(key) operation, compute the Hash(key) against each hashing function and increase the corresponding row and column index of the sketch.
For Query(key):
Calculate the Hash(key) of the input key against each hashing function.
In this case, calculate the minimum of the counter placed at the 0th row and Hash1(key)%5, 1st row and Hash2(key) % 5, and 2nd row and Hash3(key) % 5.
The minimum of all the values considered above would represent the frequency of a “key“ that appeared as part of the Insert operations.
Time complexity
Insert(key): O(d) (the time complexity for insertion is constant considering the number of hashing functions would be constant)
Query(key): O(d) (similar to insertion, this can be considered constant as well)
Space Complexity
The space complexity is O(wd) where w is the width and d is the depth of the sketch. Thus, it can be considered constant as well because it does not essentially depend on the number of keys inserted.
Now that we have understood the Insert(key) and Query(key) operations, let’s understand an example.
Suppose we are recording the vote of the user’s favorite movie. At any point, we have to tell how many votes are there for a particular movie. Refer to the following sequence of images.
Image representing an empty sketch of 3 rows and 5 columns.
For Insert(“Mission Impossible“), Let’s say,
Hash1(“Mission Impossible”) % 5 = 2
Hash2(“Mission Impossible”) % 5 = 4
Hash3(“Mission Impossible”) % 5 = 1
the sketch looks like this:
Now similarly, suppose we insert 3 more movies, like this:
Insert(“Harry Potter“) [represented by blue color]Hash1(“Harry Potter”) % 5 = 0
Hash2(“Harry Potter”) % 5 = 3
Hash3(“Harry Potter”) % 5 = 1
Insert(“Lord of the Rings“) [represented by red color]Hash1(“Lord of the Rings”) % 5 = 3
Hash2(“Lord of the Rings”) % 5 = 4
Hash3(“Lord of the Rings”) % 5 = 0
Insert(“Fast and Furious“) [represented by orange color]Hash1(“Fast and Furious”) % 5 = 2
Hash2(“Fast and Furious”) % 5 = 1
Hash3(“Fast and Furious”) % 5 = 3
The yellow boxes represent the hash collisions produced because of inserting multiple movies.
This is what the sketch looks like now:The key thing to note here is the collisions. If you now perform the Query(“Mission Impossible“) operation, the hash values would be again (2,4,1) and the minimum of those values would be 2. Now you know, even though the movie “Mission Impossible“ has been inserted only once, the frequency of it from the data structure comes out to be 2 because of the hash collisions from inserting other movies.
Also, if you perform the Query(“Fast and Furious”), the hash values would be (2,1,3) and the minimum of those would still be 1 meaning that the movie “Fast and Furious“ has only been inserted once.
Thus, as long as you select a grid that has a large number of rows meaning a decent number of hash functions being used, then collisions would be less and thus you would either get the true value or you would get a value greater than the true value of the item frequency (with some error rate).
Key Takeaways
Good Hashing functions: We must select good hashing functions that produce even and randomly distributed values among the hash size as much as possible. So that, there are fewer collisions and the Query(key) operation outputs the true value of the frequency as much as possible.
To put some numbers into context, As per this Redis blog “The math dictates that with a depth of 10 and a width of 2000, the probability of not having an error is 99.9% and the error rate is 0.1%”. So, if you decide the width and depth, the error rate and the probability of having it is already decided.
Comparison with Bloom Filters: The implementation details of the CountMin Sketch closely resemble those of a Bloom Filter. The latter utilizes bits exclusively, as opposed to integer-based counters.
When an item is added to a Bloom Filter, hash functions determine which bits should be set to 1, regardless of their prior state. In contrast, the CountMin Sketch, designed to maintain counts rather than solely tracking presence, increments counters instead. Checking for an item's existence in a Bloom Filter involves examining the relevant bits associated with that item; if any are still 0, the item hasn't been inserted previously. Consequently, Bloom Filter lookup can be likened to computing the minimum value among the relevant bits, mirroring the Count operation in a CountMin Sketch.
The tendency of the CountMin Sketch to overestimate frequency counts corresponds to the Bloom Filter's characteristic of occasionally producing false positives.
Use Cases
All other use cases where frequency count needs to be answered as fast as possible at the expense of little inaccuracy.
Conclusion
The count-min sketch is a great example of what probabilistic data structures can help you achieve just by using some hashing functions. If your service/product use case is okay to face some % of error rate, then the count-min sketch is a perfect data structure to find the frequency of an item.
That’s it, folks for this edition of the newsletter. Please consider liking and sharing with your friends as it motivates me to bring you good content for free.
Resources
Count-min sketch by Wikipedia
Count-min sketch by Redis
Count-min sketch by GeeksforGeeks
A lighter version of the official white paper for the Count-min sketch






Amazing article!!
How do we decide d and w if using this data structure? What is the best way to estimate?